Find GCD By Euclidean Algorithm Python Program

Find GCD By Euclidean Algorithm – Write a Python program to find the greatest common divisor (GCD) of two numbers using the Euclidean algorithm.

Find GCD By Euclidean Algorithm

The Euclidean algorithm

The Euclidean algorithm is a method for finding the greatest common divisor (GCD) of two integers. The algorithm is based on the principle that the GCD of two numbers remains the same if you repeatedly replace the larger number with the remainder obtained by dividing the larger number by the smaller number. This process continues until the smaller number becomes zero, at which point the GCD is the remaining larger number.

The Euclidean algorithm can be described in the following steps:

1. Given two integers a and b, where a is greater than or equal to b.
2. Calculate the remainder of a divided by b and assign it to a temporary variable r. (This can be expressed as r = a % b.)
3. If r is not equal to zero, set a to b and b to r, and go back to step 2.
4. When r becomes zero, the GCD of the original a and b is the final value of b. You can return b as the result.

This process is efficient and widely used to find the GCD of two integers. It’s known as the Euclidean algorithm because it was first described by the ancient Greek mathematician Euclid in his work “Elements” around 300 BCE. The algorithm remains a fundamental concept in number theory and is used in various mathematical and computational applications.

Source Code

# Function to count vowels in a sentence
def count_vowels(sentence):
    vowels = "aeiouAEIOU"
    vowel_count = 0

    for char in sentence:
        if char in vowels:
            vowel_count += 1

    return vowel_count

# Input from the user
user_sentence = input("Enter a sentence: ")

# Call the count_vowels function and display the result
vowel_count = count_vowels(user_sentence)
print("Number of vowels in the sentence:", vowel_count)

Output

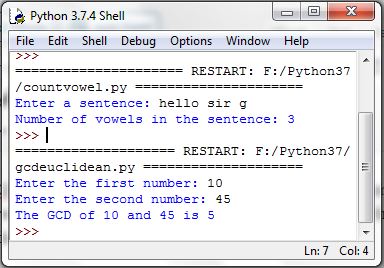
Enter the first number: 10
Enter the second number: 45
The GCD of 10 and 45 is 5

In this program:

1. We define a function find_gcd that takes two integers, a and b, as arguments.
2. Inside the function, we use a while loop to implement the Euclidean algorithm. The algorithm repeatedly updates the values of a and b until b becomes 0. At this point, the GCD is the final value of a.
3. The user is prompted to enter two numbers, num1 and num2.
4. We then call the find_gcd function with these two numbers and display the result, which is the GCD of num1 and num2.

You can use this program to find the GCD of any two integers entered by the user.