Topic: 4 C Programs Find GCD and LCM
The Greatest Common Divisor – GCD
The greatest common divisor (GCD) of two integers is the
largest positive integer dividing both.
In mathematics, the greatest common divisor (gcd) of two or
more integers, is the largest positive integer that divides each of
the integers. For example, the gcd of 8 and 12 is 4.
4 C Programs to Find GCD by loop and recursion Find LCM by Loop and GCD Formula
Because: Divisors of 8 are:1,2,4,8
and Divisors of 12 are:1,2,3,4,6,12
The Common Divisors are: 1,2,4
Therefore Greatest common divisor of 8,12 is: 4
Note: GCD is also called Highest Common Facor – HCF
Problem: Find the greatest common divisor of 54 and 24?
Solution:
The divisors of 54 are:
1,2,3,6,9,18,27,54
Similarly, the divisors of 24 are:
1,2,3,4,6,8,12,24
The common divisors of 54 and 24 are:
1,2,3,6.
Hence, the greatest common divisor of 54 and 24 is: 6
Therefore we can coclude that GCD(54,24) = 6
In other words we can also say HCF(54,24) = 6
C Program to Find GCD / HCF of Two Numbers by Loop
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
/* Write a C Program to find GCD of two numbers (HCF of two numbers) */ #include <stdio.h> int main() { int num1, num2, i, gcd; printf("Enter two integer Numbers: "); scanf("%d %d", &num1, &num2); for(i=1; i <= num1 && i <= num2; i++) { /* Check if i divides the both numbers*/ if(num1%i==0 && num2%i==0) gcd = i; } printf("GCD or HCF of %d and %d is %d", num1, num2, gcd); return 0; } |
Output:
Enter two integer Numbers: 15 20
GCD or HCF of 15 and 20 is 5
C Program to Find GCD of Two Numbers by Recursion
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
/** * C program to find GCD that is HCF * of two numbers using recursion */ #include <stdio.h> /* Function declaration */ int gcd(int a, int b); int main() { int n1, n2, result; /* Show message to enter two numbers and get input of two numbers from user */ printf("Enter two numbers to find GCD:\n"); scanf("%d%d", &n1, &n2); result = gcd(n1, n2); printf("GCD of %d and %d = %d", n1, n2, result); return 0; } /** * Recursive function to find GCD of two numbers */ int gcd(int a, int b) { if(b == 0) return a; else return gcd(b, a%b); } |
Output:
Enter two numbers to find GCD:
54
24
GCD of 54 and 24 = 6
The Least Common Multiple – LCM
The Least Common Multiple of two integers a and b, is the
smallest positive integer that is divisible by both a and b.
The least common multiple (LCM) of two integers is the smallest
positive integer that is a multiple of both.
A multiple of a number is the product of that number and an
integer. For example, 10 is a multiple of 5 because 5 × 2 = 10, so 10 is divisible by 5 and 2. Because 10 is the smallest positive
integer that is divisible by both 5 and 2, it is the least common
multiple of 5 and 2.
Example: Find Least Common Multiple – LCM of 5 and 2
Multipes of 5 are: 5,10,15,20,…
Multiples of 2 are: 2,4,6,8,10,12,14,16,18,20,22,…
Common Multiples are:10, 20
Hence Least common multiple(5,2) is: 10
Problem: Find the LCM of 4 and 6?
Solution:
Find Multiples of 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40,…
Find the multiples of 6:
6, 12, 18, 24, 30, 36, 42, ….
Find Common multiples of 4 and 6:
12, 24, 36, …
Hence, the LCM(4,6) = 12
C Program To Claculate LCM of Two Numbers
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
/* C Program to Find LCM of two numbers */ #include <stdio.h> int main() { int num1, num2, max; printf("Enter two Numbers to Find LCM:"); scanf("%d %d", &num1, &num2); /* Find the maximum number of num1 and num2*/ max = (num1 > num2) ? num1 : num2; while (1) { if (max % num1 == 0 && max % num2 == 0) { printf("The LCM of %d and %d is %d.", num1, num2, max); break; } max++; } return 0; } |
Output:
Enter two Numbers to Find LCM:4 6
The LCM of 4 and 6 is 12.
Output 2:
Enter two Numbers to Find LCM:20 15
The LCM of 20 and 15 is 60.
How To Find LCM using GCD Formula?
We know that the product of the two numbers is the product of
the LCM and the GCD.
That is if a and b are two numbers then
a x b = gcd(a,b) x lcm(a,b)
This will give the required formula to get lcm(a,b) using gcd
(a,b)
lcm(a,b) = (a x b) / gcd(a,b)
EXAMPLE: Find LCM(4,6) using GCD formula
We know that LCM(a,b) = (a x b) / GCD(a,b)
Divisors of 4 are: 1,2,4
Divisors of 6 are: 1,2,3,6
Common Divisors of 4 and 6 are: 1,2
Greatest Common Divisor of 4 and 6 = 2
Therefore LCM(4, 6) = (4 x 6) / GCD(4, 6)
= 24 / 2
= 12
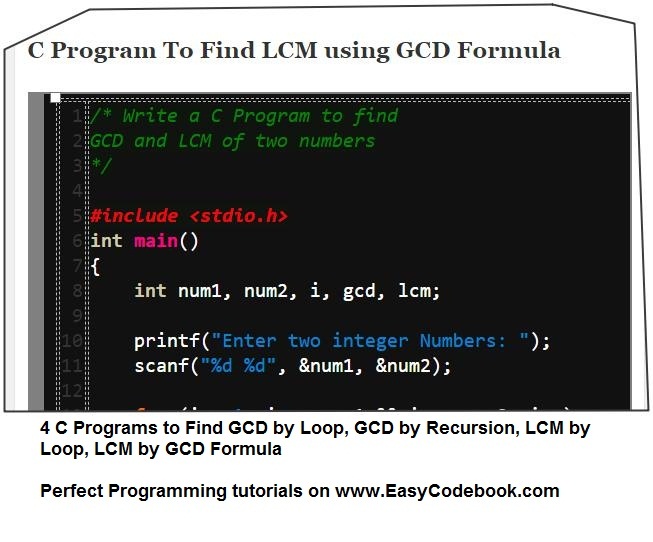
C Program To Find GCD and LCM using GCD Formula
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
/* Write a C Program to find GCD and LCM of two numbers */ #include <stdio.h> int main() { int num1, num2, i, gcd, lcm; printf("Enter two integer Numbers: "); scanf("%d %d", &num1, &num2); for (i = 1; i <= num1 && i <= num2; i++) { /* check if i divides both num1, num2*/ if (num1 % i == 0 && num2 % i == 0) gcd = i; } /* Use gcd formula to calculate LCM*/ lcm = (num1 * num2) / gcd; printf("The GCD of given two numbers %d and %d is %d.", num1, num2, gcd); printf("\nThe LCM of given two numbers %d and %d is %d.", num1, num2, lcm); return 0; } |
Output:
Enter two integer Numbers: 4 6
The GCD of given two numbers 4 and 6 is 2.
The LCM of given two numbers 4 and 6 is 12.
4 C Programs Find GCD and LCM
Learn C Language Programming by Learning These
100+ Important C Programs
![]()